
新闻活动 新闻动态
1月2日,西湖大学理学院物理系量子多体计算实验室在《Nature Communications》发表了题为 “ Addressing general measurements in quantum Monte Carlo” 的研究论文。
该工作克服了量子蒙特卡洛算法高度依赖展开表象、难以提取非对角算符信息的老大难问题,系统性地提供了一条普适解决方案。
西湖大学理学院博士生王枳妍、博士后刘泽楠一起主导并推进了该工作,博士后王哲和康复大学毛斌斌老师也为本课题做出了重要贡献。

论文地址:https://www.nature.com/articles/s41467-025-67324-0
在量子多体系统研究中,非对角物理量作为表征新奇物态与量子序的核心理论工具,具有至关重要的地位。比如非对角关联函数描述时空上的量子关联,为理解系统的宏观量子行为提供了关键视角。其在实空间的衰减行为直接定义了系统的非对角长程序,成为判断对称性破缺相变的重要依据。同时,虚时关联函数能够揭示系统激发的动力学特征。 而通过体系对称性定义的无序算符,可以揭示体系的高对称性以及其破缺。因此,系统研究各类非对角物理量,构成了探索量子多体系统相结构及其内在物理规律的理论基础。
量子蒙特卡洛(QMC)是处理大规模强关联系统最有力的无偏数值工具之一,但其“测量能力”长期受限于一个深层困境:只能高效测量在路径积分表象下的对角物理量。非对角观测量虽往往承载量子物质的核心信息,却因与采样权重“零重叠”,在传统QMC中几乎“不可见”。过去几十年仅靠“特制技巧”(如 worm 算法)解决特殊个别问题,缺乏统一框架; 这严重限制了QMC的全面应用。QMC社区亟需一个普适、严格、可编程的方案,突破舒适圈,正视非对角物理量的测量。
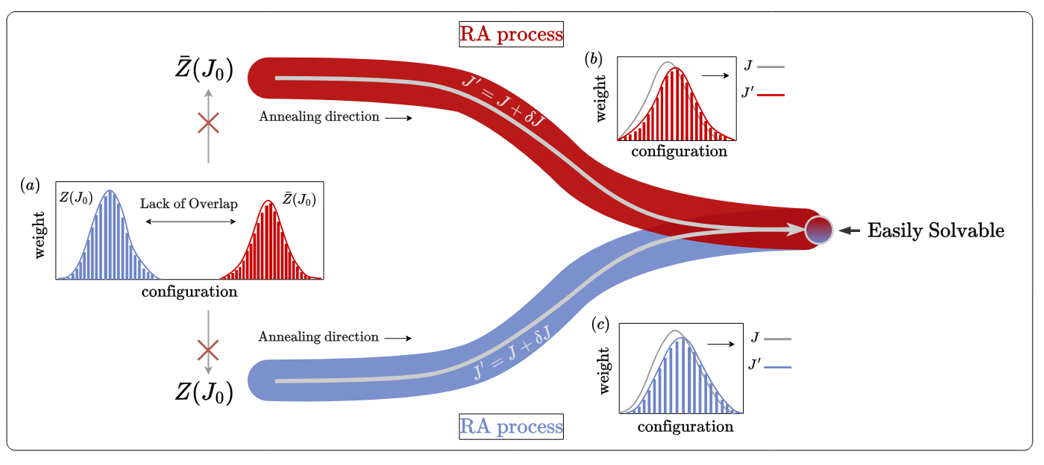
图1.双组分重赋权退火示意图。
课题组提出的“双组份重赋权退火(BRA)”框架为解决量子蒙特卡洛模拟中的核心难题提供了新思路。该方法的创新在于将任意观测量的期望值⟨O⟩表示为两个配分函数的比值形式,这一构造使得原本难以直接计算的物理量可以通过分解为两个独立部分分别处理。BRA方法的核心技术路径是沿着精心设计的连续路径对分子和分母同时进行退火重赋权采样,如Fig.1彩色路线退火所示。这一过程建立了一个系统的插值路径,将目标物理量的计算连接至一个易于求解的参考点, 如图1参考点(easily solvable)所示。参考点的选择具有灵活性,可以是小规模系统、高对称性点或可精确求解的自由理论极限等情况。 该设计的显著优势在于成功规避了传统QMC中的“零重叠”障碍,将原先难以处理的复杂比值,转化为一系列渐进、可计算的相邻比值。这一转变使得研究者能够通过连续变化的中间状态,系统性地探索物理量的演化行为,为研究传统方法难以处理的强关联系统开辟了新途径。尤为重要的是,该方法具有高度的通用性与灵活性,适用于不同模型、维度、观测量形式及QMC实现方式。研究团队在XXZ模型与横场Ising模型中成功实现了多项过去难以完成的测量,包括:
一维/二维中任意距离的等时与虚时非对角关联;
四点、多体、非局域无序算符(揭示 perimeter/area law);
将系统尺寸 L、空间距离 r、虚时间 τ 本身作为退火变量,实现“从小推大、从近推远”。
所有数值结果与精确对角化(ED)高度一致,并且验证了该方法具备无偏、高精度和强扩展性的特点。未来,该方法可进一步应用于多体虚时谱函数计算、多体纠缠响应、高阶对称性序参量识别、可标度分析及与实验数据直接对标等前沿方向。
从更广泛的视角看,BRA框架的核心思想是为两个原本因“鸿沟”阻隔而无法直接连接的问题,构建出一条连续的演化路径与计算之桥。这一思路不仅适用于量子多体计算,也有潜力应用于统计物理、大数据分析、贝叶斯推断、机器学习中的似然比估计等领域,为复杂系统的数值研究提供了一种新颖而有力的视角。

部分作者合影(左起):王哲、严正、刘泽楠、王枳妍
上述工作得到国家高层次青年人才项目、国家博士后面上项目,国自然理论物理博士后项目以及西湖大学专项经费的支持,并得到来自西湖大学高性能计算中心的计算⽀持。
















